岩通ソフトシステム株式会社はソフトウェア開発からサービスまでをトータルで提供するソリューションプロバイダです。

　算法は、数学的には計算の方法を表すそうですが、情報処理の世界ではアルゴリズムを表すことになっています。とはいっても、 算法という言葉は、情報処理の世界では、ほとんど使われなくなっていますので、言葉自体を知っている人も少なくなってきています。今はアルゴリズムと呼べば、みんなが理解できると思います。
　アルゴリズムを使う利点ですが、多くは簡単には解決できない問題を解決していて、その解法が正しいことが証明されており、さらに無料で使うことができるということだと思います。自分でアルゴリズムから考えていたら、いくら時間があっても足りないので、先人の知恵を借りるということになります。

ダイクストラ法 Dijkstra's algorithm

　算法の三つ目のコラムでは、ダイクストラ法を扱います。ダイクストラ法は、今までの深さ優先検索や幅優先検索よりも少し複雑だと思いますが、幅優先検索の発展系ととらえることができると思います。
　なお、グラフ、無向グラフ、有向グラフ、ノード、エッジなどの用語については、算法の一つ目のコラムで説明していますので、そちらをご覧ください。

　ダイクストラ法は、有向グラフ上の開始ノードから終了ノードまでの最短経路を求めることができます。アルゴリズム自体は、いろいろなところで説明されていますし、使い道についても明白なのですが、確認の意味も含めて、ここで使い道についてあえて説明すると、例えば、乗り換え案内のようなある駅からある駅に行くときの最短のルートや、最も交通費の安いルートなどを検索することができますし、道路の情報を利用して、どのルートで行くのが一番早く目的地に着けるかといった検索が可能です。ただし、電車の時刻表や道路の情報は膨大なので簡単に実現することはできないと思いますが。

　前置きが長くなってしまいましたが、ダイクストラ法について説明します。
　今回は、いきなり疑似プログラムを見ていただいても分かりにくいので、まず、動きの方から見ていただくことにします。実際にやっていることが、なんとなくわかれば、疑似プログラムを理解するのが簡単になります。
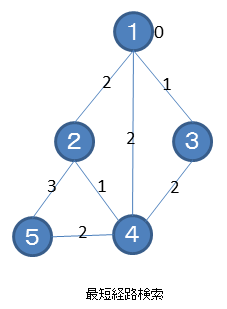
　下の図を見てください。下の図は、ダイクストラ法を説明するのに使用する有向グラフです。今回は、エッジに方向を示す矢印を記述していませんが、すべてのエッジは双方向に行くことが可能としています。実際の電車や道路も、通常は双方向に行くことが可能ですね。スタートノードは1番のノードで、最終ノードは5番のノードです。各エッジに数字が打ってありますが、これが重みです。例えば、所要時間、運賃、距離などに相当します。ノード１の横に記述された数字は、スタートノードからノード１への重みの合計を示します。ノード１はスタートノードですから、当然重みは０になります。他のノードには重みの合計が記述されていませんが、初期値として十分大きな値を設定してあるとします。
　それでは、ノード１からスタートしてノード５に行く一番重みが少ないルートをどうやって見つけるか（実際に求まるのは、そのルートを通った時の重みの合計値ですが）を説明をします。

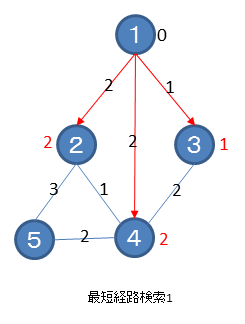
　未訪問で一番重みの少ないノードを探します。下図ではノード１が選択されます。ノード１の全エッジについて行き先のノードの重みとしてノード１の重みとエッジにつけられた重みの合計値が、もともとの重みよりも小さい時に求めた合計値を設定します。下図では、ノード２、ノード３、ノード４に重みが設定されます。なお、訪問したノードには赤い印をつけて区別できるようにしておきます。

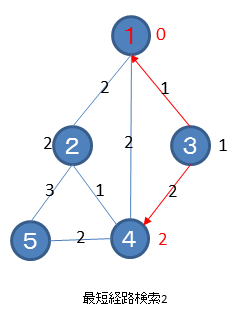
　未訪問で一番重みの少ないノードを探します。ノード１は既に訪問済なので、下図ではノード３が選択されます。ノード３の全エッジについて行き先のノードの重みとして、ノード３の重みとエッジにつけられた重みの合計値が、もともとの重みよりも小さい時に求めた合計値を設定します。下図では、ノード１は設定済の重みが０ですから変更されず、ノード４も設定済の重みが２で、今回求めた合計値が３なので変更されません。

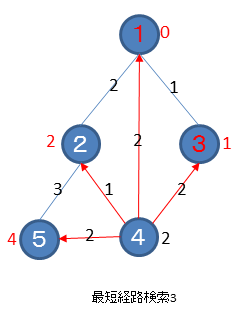
　未訪問で一番重みの少ないノードを探します。下図ではノード４が選択されます。ノード４の全エッジについて行き先のノードの重みとして、ノード４の重みとエッジにつけられた重みの合計値が、もともとの重みよりも小さい時に求めた合計値を設定します。下図では、ノード１は設定済の重みが０ですから変更されず、ノード２も設定済の重みが２で、今回求めた合計値が３なので変更されず、ノード３も設定済の重みが１で、今回求めた合計値が４なので変更されず、ノード５は設定済の重みが十分大きく、今回求めた合計値が４なので設定します。

　未訪問で一番重みの少ないノードを探します。下図ではノード２が選択されます。ノード２の全エッジについて行き先のノードの重みとして、ノード４の重みとエッジにつけられた重みの合計値が、もともとの重みよりも小さい時に求めた合計値を設定します。下図では、ノード１は設定済の重みが０ですから変更されず、ノード４も設定済の重みが２で、今回求めた合計値が３なので変更されず、ノード５も設定済の重みが４で、今回求めた合計値が５なので変更されません。

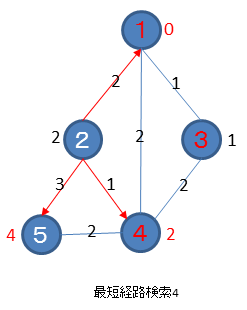
　未訪問で一番重みの少ないノードを探します。下図ではノード５が選択されます。ノード５の全エッジについて行き先のノードの重みとして、ノード５の重みとエッジにつけられた重みの合計値が、もともとの重みよりも小さい時に求めた合計値を設定します。下図では、ノード２は設定済の重みが２で、今回求めた合計値が７なので変更されず、ノード４も設定済の重みが２で、今回求めた合計値が６なので変更されません。

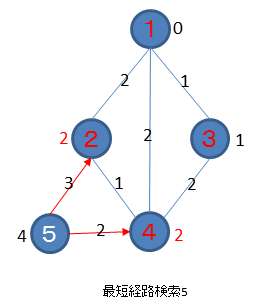
　未訪問で一番重みの少ないノードを探しますが、もう未訪問のノードはありませんから、ここでアルゴリズムを終了します。この時に、ノード５に設定された重みの４が求める答えの最短ルートを通った時の重みとなります。

　疑似プログラムを使用して処理を説明します。前提として、各ノードは複数のエッジをリンクできるデータ構造を持っており、各エッジは行き先のノードをリンクできるデータ構造を持っているものとします。また、ノードとエッジには重みを格納できるように、ノードには訪問した印を付けられるようにしておきます。

DA（スタートノード、ゴールノード） ｛

　　全てのノードに未訪問と重みとして十分大きな値を設定します。

　　処理対象のノード（下記参照）がある限り繰り返します。｛
　　　　未訪問で重みが十分大きくないノードの中で一番重みが小さいノードを処理対象のノードとします。
　　　　処理対象のノードが見つからなければ、繰り返しを抜けます。
　　　　処理対象ノードのすべてのエッジについて繰り返します。｛
　　　　　　処理対象のノードの重みとエッジの重みを足したものが、行き先のノードに設定済の重みよりも小さければ、
　　　　　　行き先ノードの重みに小さい重み（上で加算した重み）を設定します。
　　　　｝
　　｝
　呼び出し元にゴールノードの重みを返します。
｝

　上のアルゴリズムを使う限り、グラフがループしている場合でも、アルゴリズムはループすることはありません。なお、乗り換え案内のような目的で使う場合には、時間と料金のような複数の重みが必要になったり、途中で前の列車を追い越すような列車の考慮も必要になりますから、アルゴリズムは複雑になりますが、基本は上で説明したアルゴリズムを使用して、あとは課題に合わせて応用問題を解いていくということになると思います。

　ダイクストラ法は、実生活に結びついた多くの問題を解くことができるので、知っていると便利なアルゴリズムの一つです。